Demos

We have packaged several demo applications with the source code to show some potential uses. These are all available in the src/demos directory and include:

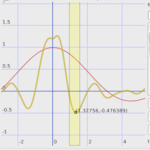
Artistic control is very important for film making. Expressions though essentially a mathematical concept can readily be used to create artist directed procedural content.

One key we found was creating an interface around the expression language that automatically exposed parameters on defined variables.

We have included in src/demos a simple Qt image editor (.mov) to illustrate this functionality.

editor

In the example, you can see a color ramp, slider, and spline ramp that are all automatically generated from just typing the expression below the widgets.

Also, libraries of expressions can be created by expert users and shared with other users. Take a look at our expression library (.mov) in action.

library

Another demonstration of the expression editor can be seen in this video (YouTube) at time 3:18.

Usage Examples

Noise Driving Color Interpolation

SeExpr can be used in many evaluation contexts, and in each context it may have different bound variables, different customizable functions. As an example, a programmer could allow a user to generate an image by evaluating an expression at each point of the image and binding a u and v variable for the u,v parameter of the image. Then the user could write examples like the following:

Noise Example 1

$val=noise(10*$u,10*$v);
$color=ccurve($val,  
    0.000, [1.000, 1.000, 0.498], 4,  
    0.590, [0.333, 0.000, 0.000], 4,  
    0.665, [1.000, 1.000, 0.000], 4);

$color

Noise Example 2

$val=voronoi(5*[$u,$v,.5],4,.6,.2);
$color=ccurve($val,
    0.000, [0.141, 0.059, 0.051], 4, 
    0.185, [0.302, 0.176, 0.122], 4, 
    0.301, [0.651, 0.447, 0.165], 4,  
    0.462, [0.976, 0.976, 0.976], 4);
$color

Ray Tracing Sphere

This is an example of something you probably should not do with expressions. At the same time it is sometimes nice to prototype functions and techniques in expressions because of the interactivity. 

$Cs=[1.000, 0.000, 1.000]; # Sphere Color
$L1=norm([-1.3,-.3,0]); # Light Direction 1
$L2=norm([.8,-1,-1]); # Light Direction 2
$sp=[0.000, 0.000, -3.000]; # Sphere center
$d=norm([$u-.5,$v-.5,-1]); # ray direction
$o=[0.000, 0.000, 0.000]; # ray origin
$r=1.000; # sphere radius
# quadratic coefficients
$a=dot($d,$d);
$ominussp=$o-$sp;
$b=2*dot($d,$ominussp);
$c=dot($ominussp,$ominussp)-$r*$r;
# discriminant
$disc=$b*$b-4*$a*$c;
$color=0.000;
if($disc>0){ # two hit case
  # minimum ray parameter
  $t=min((-$b+sqrt($disc))/(2*$a),(-$b-sqrt($disc))/(2*$a))[0];
  if($t>=0){ # if we are in front of camera
      $Pintersect=$o+$d*$t;  # point of intersection
      $N=norm($Pintersect-$sp); # intersection normal
      # lighting
      $H1=(-$L1+-$d)/length($L1+$d);
      $color=max(dot($N,-$L1),0)*($Cs*.3+.5*max(0,dot($H1,$N))^80);
      $H2=(-$L2+-$d)/length($L2+$d);
      $color+=max(dot($N,-$L2),0)*($Cs*.3+.5*max(0,dot($H2,$N))^80);
   }
}
# return color
$color